EDFA is the core functional device in the optical transmission system. It has the advantages of high gain, large bandwidth, low noise, insensitive to optical polarization state, transparent to data rate and format, and negligible channel crosstalk in multi-channel systems. . The combination of DWDM and EDFA can not only improve the capacity of the system, but also have high flexibility and economy. However, due to the dense multiplexing of wavelengths of each channel and the uniform broadening characteristics of EDFA, there is fierce competition between different channels, and the gain and spectral line shape of EDFA need to be kept stable, so the problems of EDFA gain control and flatness are introduced. At present, there are mainly technical means to achieve EDFA gain flattening, such as thin-film filtering, low-light sine filtering, and fiber grating filtering. The optical gain flattening filter GFF is based on mature thin-film filtering technology, and is used in EDFA to compensate for uneven gain amplification under different DWDM channels. Figure 1 shows the working principle of the GFF diaphragm.
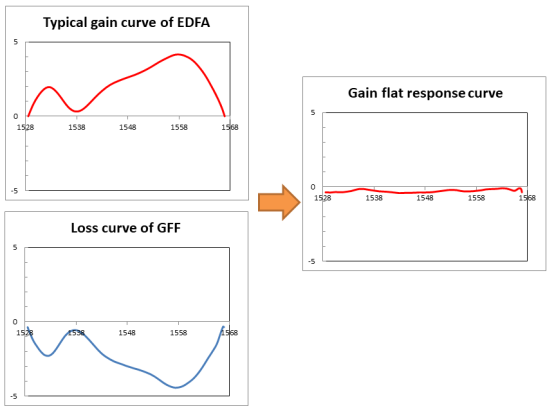
The gain-flat response curve through GFF mainly depends on the following important parameters:
1. Working wavelength: λrange = λmax – λmin (minimum and maximum wavelength in target band)
2. Additional loss: EL (dB) = minimum(ILEF)
3. Error function: ILEF (dB) = IL– ILtgt
4. Peak-to-peak error function: ILEFrange (dB) = ILEFmax – ILEFmin
The peak-to-peak error function (ILEFrange) represents the maximum flatness of the transmitted signal by comparing the spectral performance of the fabricated filter to the target curve, which describes the quality of a GFF filter. In general, the determining factor for achieving the smallest ILEFrange is the maximum slope and smoothness of the target curve. Some applications require multiple flat areas, or additional passbands outside the flat areas; these may increase filter complexity.
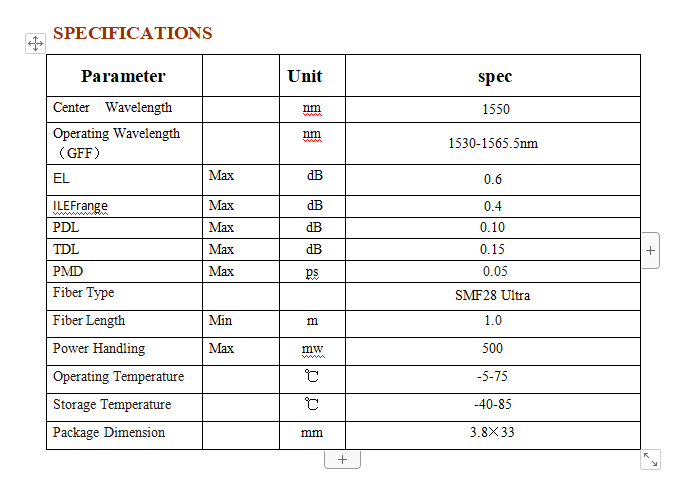
The gain spectral lines of different EDFAs are not the same, so the transmittance curves of the GFF filters are not exactly the same. We take this device as an example, and its parameter performance is shown in Table 1.